Problema 6

Se desea construir un depósito cilíndrico cerrado de área total igual a $54 \: m^2$. Determina el radio de la base y la altura del cilindro para que este tenga volumen máximo.

Necesitamos recordar algunos conocimientos previos:

• Área del círculo: $\pi R^2$
• Longitud de la circunferencia: $2 \pi R$
• Volumen del cilindro: Área_base · Altura: $\pi R^2 \cdot H$
• Área del cilindro: 1 rectángulo + 2 círculos: $2 \pi R \cdot H + 2 \cdot \pi R^2$

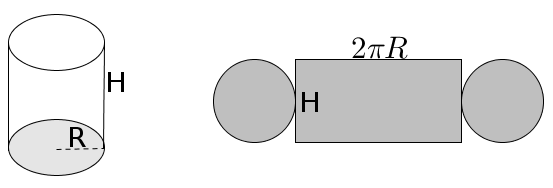
Datos del problema:

• Área del cilindro es $54$
  $$2 \pi R \cdot H + 2 \cdot \pi R^2 = 54$$
• El volumen debe ser máximo
  $$\mathrm{Volumen} = \pi R^2 \cdot H$$

La función a maximizar (el volumen) tiene dos variables: $R$ y $H$.
Debemos expresarlo con una sola variable.
Para ello, debemos poner una variable en función de otra. Nos ayudamos de la fórmula del área: $2 \pi R \cdot H + 2 \cdot \pi R^2 = 54$, donde despejaremos $H$.

$$H=\frac{54-2 \pi R^2}{2 \pi R}$$
Sustituimos en el volumen, con lo cual nos quedará ya una función con una sola variable
$$\mathrm{Volumen}\rightarrow V(r)=\pi R^2 \cdot \frac{54-2 \pi R^2}{2 \pi R}$$

Simplificando y ordenando nos queda:
$$V(r) = -\pi R^3+27R$$

Para buscarle un máximo debemos igualar la primera derivada a cero y resolver la ecuación. Las soluciones serán los candidatos a máximos y mínimos.
Aplicándole la segunda derivada (y mirando su signo), sabremos si ese máximo o mínimo.
$$V^{\prime}(r) = -3 \pi R^2 + 27 = 0 \Rightarrow R = \pm \frac{3}{\sqrt{\pi}}$$

Podemos descartar la solución negativa por ser $R$ una longitud.
$$V^{\prime\prime}(r)=-6 \pi R$$
$$V^{\prime\prime}(\frac{3}{\sqrt{\pi}}) < 0 \Longrightarrow \frac{3}{\sqrt{\pi}}$$ es MÁXIMO

Ya conocemos el radio $R = \frac{3}{\sqrt{\pi}}=\frac{3 \sqrt{\pi}}{\pi}$,
ahora calculamos la altura $H$.

$$H=\frac{54-2 \pi R^2}{2 \pi R}=\frac{54-2 \pi \left( \frac{3}{\sqrt{\pi}} \right)^2}{2 \pi \cdot \frac{3}{\sqrt{\pi}}} \Rightarrow H=\frac{6 \sqrt{\pi}}{\pi}$$