Problema 4 examen matemàtiques II 5 juny 2020

Sea $f$ la función definida para $x \neq 1$ por $f(x) = \displaystyle\frac{2x^2}{x-1}$

Determina las asíntotas de la gráfica de $f$

Asíntota vertical $\boxed{x=1}$ porque $\lim\limits_{x \rightarrow 1} f(x) = \infty$

Asíntota horizontal NO HAY porque $\lim\limits_{x \rightarrow \infty} f(x) = \infty$

La asíntota oblicua es una recta de ecuación $y=mx+n$ , donde $m$ y $n$ se calculan con las expresiones siguientes:

$$m = \lim\limits_{x \rightarrow \infty} \frac{f(x)}{x}$$
$$n = \lim\limits_{x \rightarrow \infty} \left[f(x) -mx\right]$$

Si lo aplicamos a la función $f(x)$ obtenemos:
$$m = \lim\limits_{x \rightarrow \infty} \frac{\frac{2x^2}{x}}{x}=\lim\limits_{x \rightarrow \infty} \frac{2x^2}{x^2-x}=2$$
$$n = \lim\limits_{x \rightarrow \infty} \left[\frac{2x^2}{x-1} -2x\right] = \lim\limits_{x \rightarrow \infty} \frac{2x}{x-1}=2$$

La Asíntota oblicua es $\boxed{y=2x+2}$

Determina los intervalos de crecimiento y decrecimiento y los extremos relativos de $f$

Monotonía y extremos
$$f'(x)=0 \Rightarrow \frac{2x^2-4x}{(x-1)^2}=0 \Rightarrow x=0 ; x=2$$
Los intervalos a considerar son $(-\infty,0)$ , $(0,2)$ y $(2,+\infty)$

Si aplicamos $f'(x)$ a un punto de cada intervalo obtenemos:

• $f'(-1)=1.5 > 0 \rightarrow$ es creciente en $(-\infty,0)$
• $f'(0.5)=-6 < 0 \rightarrow$ es decreciente en $(0,2)$
• $f'(3)=1.5 > 0 \rightarrow$ es creciente en $(2, +\infty)$

Como la función es continua en cada uno de lo tres nitervalos, concluimos que hay un máximo en $x=0$ y un mínimo en $x=2$.
Calculamos la segunda coordenada:
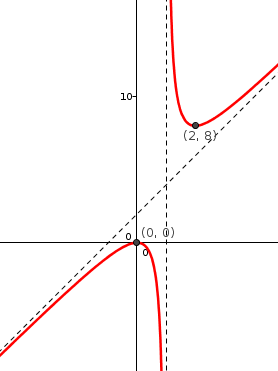
$$f(0)=0 \rightarrow MAX(0,0)$$
$$f(2)=8 \rightarrow MIN(2,8)$$

Esboza la gráfica de $f$