Problema 3 examen matemàtiques CCSS 04 juny 2020

Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar $1600$ personas y $96$ toneladas de equipaje. Los aviones disponibles son de dos tipos: $11$ del tipo $A$ y $8$ del tipo $B$. La contratación de un avión del tipo $A$ cuesta $4$ millones de pts y puede transportar $200$ personas y $6$ toneladas de equipaje; la contratación de uno del tipo $B$ cuesta $1$ millón de pts y puede transportar $100$ personas y $15$ toneladas de equipaje. ¿Cuántos aviones de cada tipo deben utilizarse para que el coste sea mínimo?.

Veamos una tabla con los datos:

La función objetivo sería: $F(x,y)=4x+y$

La primera de las inecuaciones se puede simplificar (dividiendo todo por $100$) y quedaría: $2x+y \geq 16$

Dibujamos el recinto y calculamos los vértices

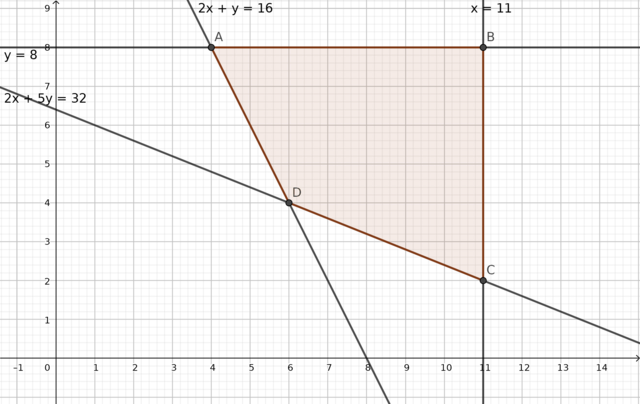
Cada uno de los vértices es la intersección de dos rectas (si resolvemos el sistema de ecuaciones formado por las ecuaciones de las dos rectas obtenemos los valores del vértice).

Una vez calculados obtenemos los siguientes vértices:

• $A(4,8)$
• $B(11,8)$
• $C(11,2)$
• $D(6,4)$

Aplicamos la función objetivo a cada uno de los vértices:

• $F(4,8) = 4 \cdot 4 + 8 = 24$
• $F(11,8) = 4 \cdot 11 + 8 = 52$
• $F(11,2) = 4 \cdot 11 + 2 = 46$
• $F(6,4) = 4 \cdot 6 + 4 = 28$

El coste mínimo ($24$ millones) se obtendría contratando $4$ aviones de tipo A y $8$ aviones de tipo B.