Problema de camp i potencial elèctric

Disposem d’una distribució de tres càrregues puntuals amb càrrega $\boldsymbol{q_1 = +25q}$, $\boldsymbol{q_2 = -81q}$ i $\boldsymbol{q_3 = +18q}$ respectivament, on el valor de $\boldsymbol{q}$ és positiu però desconegut. Les càrregues estan distribuïdes segons s’indica a la figura 1:

Es demana:

Calculeu el camp electrostàtic resultant al punt $\boldsymbol{P = (3a, 0)}$ (considereu $\boldsymbol{a > 0}$ per a tot el problema).

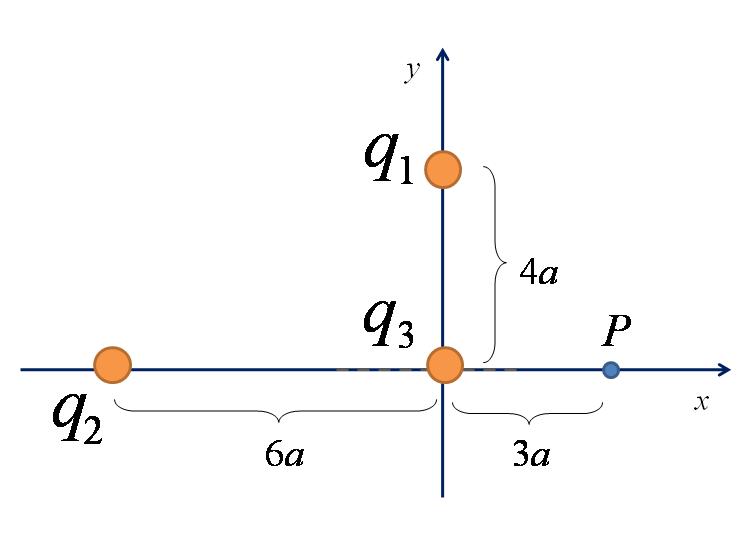
Calcularem el camp elèctric mitjançant el principi de superposició

\begin{equation}\vec{E}=\frac{1}{4 \pi\epsilon_0}\sum_{i=1}^{3}\frac{q_i}{\left| \vec{r}-\vec{r}i \right|^2}\widehat{u}_{\vec{r}-\vec{r}_i}\end{equation}

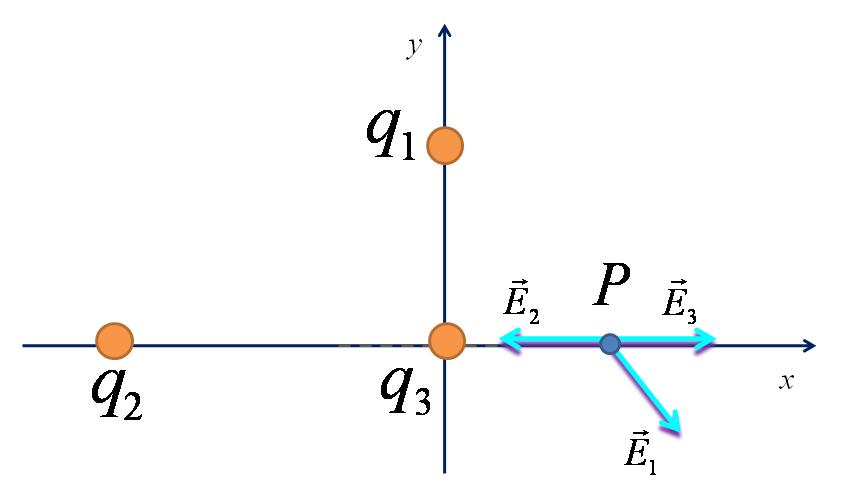
Les contribucions al camp de cada càrrega les podeu observar a la figura 2, on s’ha tingut en compte que, el camp $\vec{E}$, surt d’una càrrega positiva i entra en una negativa.

El càlcul dels vectors de posició és directe a partir de la figura 1 anterior quedant com segueix

\begin{equation}
\vec{r}=3a\vec{i}+0\vec{j}=3a\vec{i}
\end{equation}
\begin{equation}
\vec{r}_1=0\vec{i}+4a\vec{j}=4a\vec{j}
\end{equation}
\begin{equation}
\vec{r}_2=-6a\vec{i}+0\vec{j}=-6a\vec{i}
\end{equation}
\begin{equation}
\vec{r}_3=0\vec{i}+0\vec{j}
\end{equation}

Els vectors relatius vindran donats per la resta del vector de posició del punt on calculem el camp menys el vector de posició de la càrrega considerada

\begin{equation}
\vec{r}-\vec{r}_1=3a\vec{i}-4a\vec{j}\longrightarrow\boxed{\left| \vec{r}-\vec{r}_1 \right|}=\sqrt{(3a)^2+(-4a)^2}=\boxed{5a}
\end{equation}
\begin{equation}
\vec{r}-\vec{r}_2=9a\vec{i}+0\vec{j}\longrightarrow\boxed{\left| \vec{r}-\vec{r}_2 \right|}=\sqrt{(9a)^2+(0)^2}=\boxed{9a}
\end{equation}
\begin{equation}
\vec{r}-\vec{r}_3=3a\vec{i}+0\vec{j}\longrightarrow\boxed{\left| \vec{r}-\vec{r}_3 \right|}=\sqrt{(3a)^2+(0)^2}=\boxed{3a}
\end{equation}

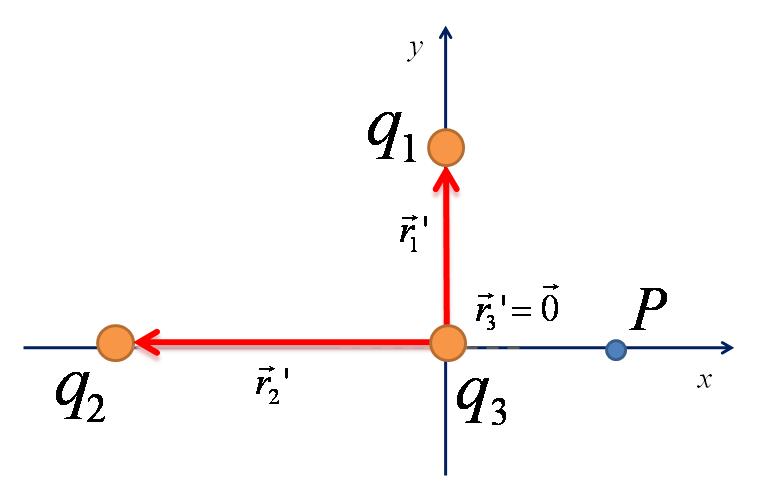
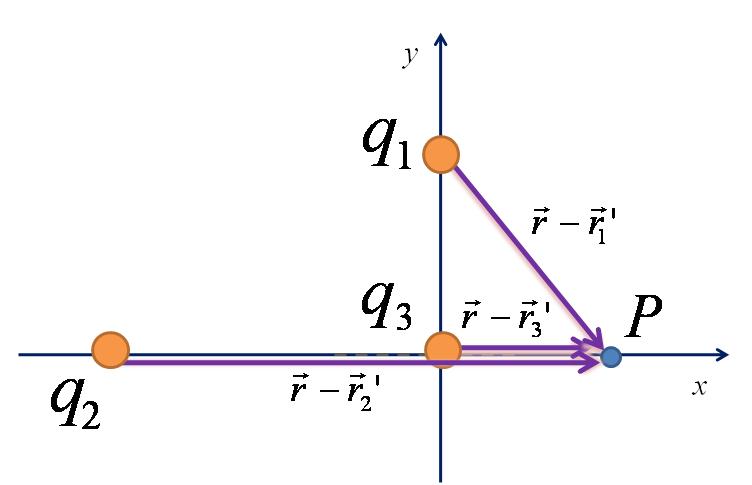
Els vectors relatius unitaris vindran donats en dividir cada vector relatiu pel seu mòdul:

\begin{equation}\boxed{\widehat{u}{\vec{r}-\vec{r}_1}}=\frac{\vec{r}-\vec{r}_1}{\left| \vec{r}-\vec{r}_1 \right|}=\boxed{\frac{1}{5}(3\vec{i}-4\vec{j})} \end{equation} \begin{equation} \boxed{\widehat{u}{\vec{r}-\vec{r}2}}=\frac{\vec{r}-\vec{r}_1}{\left| \vec{r}-\vec{r}_2\right|}=\frac{1}{9}(9\vec{i})=\boxed{\vec{i}} \end{equation} \begin{equation} \boxed{\widehat{u}{\vec{r}-\vec{r}_3}}=\frac{\vec{r}-\vec{r}_1}{\left| \vec{r}-\vec{r}_3\right|}=\frac{1}{3}(3\vec{i})=\boxed{\vec{i}}\end{equation}

Volem el camp electrostàtic E al punt $P$, per tant, utilitzant l’equació (1) obtenim:

\begin{equation}\boxed{\vec{E}P}=\frac{1}{4 \pi\epsilon_0}\sum{i=1}^{3}\frac{q_i}{\left| \vec{r}-\vec{r}i \right|^2}\widehat{u}{\vec{r}-\vec{r}_i}=\cdots=\boxed{\frac{q}{5\pi\epsilon_0a^2}(2\vec{i}-\vec{j})}\end{equation}

Calculeu el valor necessari de $\boldsymbol{q}$ per tal que el potencial elèctric resultant al punt $\boldsymbol{P}$ anterior sigui de $\boldsymbol{10\ \text{V}}$.

El potencial elèctric ve donat per la següent expressió:

\begin{equation}V_P=\frac{1}{a\pi\epsilon_0}\sum_{i=1}^3\frac{q_i}{\left| \vec{r}-\vec{r}_i \right|}\end{equation}

el vector de posició del punt on estudiem el potencial continua sent el vector de posició del punt $P$:

\begin{equation}\vec{r}=3a\vec{i}\end{equation}

i els mòduls dels vectors relatius entre càrrega considerada i punt on calculem el potencial són els mateixos que teníem a l’apartat (a):

\begin{equation}
\left| \vec{r}-\vec{r}_1 \right|=5a
\end{equation}
\begin{equation}
\left| \vec{r}-\vec{r}_2 \right|=9a
\end{equation}
\begin{equation}
\left| \vec{r}-\vec{r}_3 \right|=3a
\end{equation}

Per tant, utilitzant l’equació (13)

\begin{equation}\boxed{V_P}=\frac{1}{4\pi\epsilon_0}\sum_{i=1}^3\frac{q_i}{\left| \vec{r}-\vec{r}_i \right|}=\cdots=\boxed{\frac{q}{2\pi\epsilon_0a}\ \text{V}}\end{equation}

Finalment, igualant aquest resultat al voltatge donat a l’enunciat podem aïllar la densitat de càrrega demanada:

\begin{equation}
10\ \text{V}=\frac{q}{2\pi\epsilon_0a}\ \text{V}\longrightarrow\boxed{q=20\pi\epsilon_oa\ \text{C}}
\end{equation}

que té un valor positiu