Càlcul d’àrea. Problema 4

Considera les funcions $f:\mathbb{R}\longrightarrow\mathbb{R}$ i $g:\mathbb{R}-{0}\longrightarrow\mathbb{R}$ definides per $f(x)=5-x^2$ i $g (x)=\dfrac{4}{x^2}$.

Esbossa les gràfiques de les dues funcions i calcula els punts de tall entre elles.

$\boxed{f(x)=5-x^2}$ és una paràbola (funció quadràtica)

• Oberta per baix $\cap$, perquè és el coeficient de $x^2$ menor que zero.
• Vèrtex: $x=\dfrac{-b}{2a}=\dfrac{0}{2\cdot(-1)}=0 \Rightarrow \boxed{(0,5)}$
• Punts de tall amb l’eix $X: 5-x^2=0 \Rightarrow x=\pm\sqrt{5} \Rightarrow \boxed{(-\sqrt{5},0)}$ i $\boxed{(+\sqrt {5},0)}$
• Punt de tall amb l’eix $Y: x=0 \Rightarrow \boxed{(0,5)}$

$\boxed{g(x)=\dfrac{4}{x^2}}$ és una hipèrbola

• amb $\lim\limits_{x\to\pm\infty}g(x)=\dfrac{4}{+\infty}=0^+$, asímptote horitzontal $y=0$.
• $\lim\limits_{x\to0^-}=\dfrac{4}{0^+}=+\infty i \lim\limits_{x\to0^+}=\dfrac{4}{0^+}= +\infty \Rightarrow x=0$ asímptota vertical.

Punts de tall:

$f(x)=g(x) \Rightarrow 5-x^2=\dfrac{4}{x^2} \Rightarrow 5x^2-x^4=4 \Rightarrow x^4-5x^2+4= 0$ equació biquadrada.

Sigueu $t=x^2 \Rightarrow t^2-5t+4=0 \Rightarrow (t-1)(t-4)=0 \Rightarrow \left\{\begin{array}{l} t=1 \Rightarrow x=\pm1 \ t=4 \Rightarrow x=\pm2 \end{array}\right.$

Els punts de tall són $(-1,4)$, $(1,4)$, $(-2,1)$ i $(2,1)$.

Fem l’esbós:

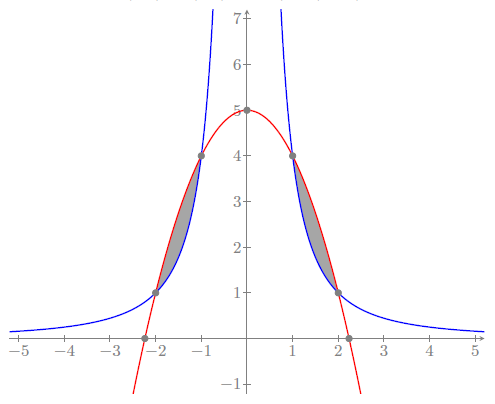
Calcula la suma de les àrees dels recintes limitats per les gràfiques de $f$ i $g$.

$$\text{Àrea}=\int_{-2}^{-1}\left(f(x)-g(x)\right)\ dx + \int_1^2\left(f(x)-g(x)\right)\ dx =$$

$$=\int_{-2}^{-1}\left(5-x^2-\dfrac{4}{x^2}\right)\ dx + \int_1^2\left(5-x^2-\dfrac{4}{x^2}\right)\ dx =$$

$$= \left[5x-\dfrac{x^3}{3}+\dfrac{4}{x}\right]_{-2}^{-1} + \left[5x-\dfrac{x^3}{3}+\dfrac{4}{x}\right]_1^2=$$

$$=\left(\left(-5+\dfrac{1}{3}-4\right)-\left(-10+\dfrac{8}{3}-2\right)\right)+\left(\left(10-\dfrac{8}{3}+2\right)-\left(5-\dfrac{1}{3}+4\right)\right)=$$

$$=\left(3-\dfrac{7}{3}\right)+\left(3-\dfrac{7}{3}\right)=6-\dfrac{14}{3}=\dfrac{4}{3}\ u^2$$

$$\boxed{\text{Àrea}=\dfrac{4}{3}\ u^2}$$