Problema d’optimització d’una porta

Es vol fer una porta rectangular coronada per un semicercle com el de la figura. El buit de la porta ha de tenir $16$ metres quadrats. Si és possible, determineu la base $x$ perquè el perímetre sigui mínim.

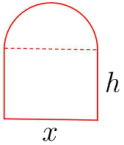
La porta està formada per un rectangle de $\text{àrea}=x\cdot h$ i mitja circumferència de diàmetre $x$, l’àrea del qual és $\dfrac{\pi\cdot\left(\frac{x}{2}\right) ^2}{2}=\dfrac{\pi\cdot x^2}{8}$

L’àrea total de la porta és $x\cdot h+\dfrac{\pi\cdot x^2}{8}$

Com ha de ser de $16$ metres quadrats:

$$\Rightarrow\hspace{5pt} x\cdot h+\dfrac{\pi\cdot x^2}{8}=16 \hspace{5pt}\Rightarrow\hspace{5pt} \boxed{8xh+\pi\cdot x^2 =128}$$

$$\Rightarrow\hspace{5pt}h=\dfrac{128}{8x}-\dfrac{\pi\cdot x^2}{8x} \hspace{5pt}\Rightarrow\hspace{5pt} \boxed{h=\ dfrac{16}{x}-\dfrac{\pi}{8}x}$$

El perímetre d’aquesta figura serà $2h+x+\dfrac{2\pi\frac{x}{2}}{2}=2h+x+\dfrac{\pi\cdot x}{2}$

$$\Rightarrow\hspace{5pt} \text{perímetre}=p(x)=2\cdot\left(\dfrac{16}{x}-\dfrac{\pi}{8}x\right)+ x+\dfrac{\pi\cdot x}{2}=\dfrac{32}{x}-\dfrac{\pi}{4}x+x+\dfrac{\pi\cdot x}{2}$$

$$\Rightarrow\hspace{5pt} p(x)=\dfrac{32}{x}-\dfrac{\pi}{4}x+\dfrac{\pi}{2}x+x \hspace{5pt}\Rightarrow \hspace{5pt} \boxed{p(x)=\dfrac{32}{x}+\dfrac{\pi}{4}x+x}$$

Derivem la funció perímetre per buscar el seu mínim.

$$p'(x)=\dfrac{-32}{x^2}+\dfrac{\pi}{4}+1$$

Igualem a $0$: $$\dfrac{-32}{x^2}+\dfrac{\pi}{4}+1=0 \hspace{5pt}\Rightarrow\hspace{5pt} \dfrac{\pi}{4} +1=\dfrac{32}{x^2} \hspace{5pt}\Rightarrow\hspace{5pt} \pi x^2+4x^2=128 \hspace{5pt}\Rightarrow$$

$$\Rightarrow\hspace{5pt} x^2\left(\pi+4\right)=128 \hspace{5pt}\Rightarrow\hspace{5pt} x^2=\dfrac{128}{\pi+4} \hspace{5pt}\Rightarrow\hspace{5pt} x=\pm\sqrt{\dfrac{128}{\pi+4}}$$

$x$ ha de ser positiu, $\Rightarrow\hspace{5pt}x=+\sqrt{\dfrac{128}{\pi+4}}$, vegem si minimitza la funció:

$$p”(x)=\dfrac{-(-32)\cdot2x}{(x^2)^2}=\dfrac{64x}{x^4}=\dfrac{64}{x^3}$$

$p”\left(+\sqrt{\dfrac{128}{\pi+4}}\right)=\dfrac{64}{\left(+\sqrt{\dfrac{128}{\pi+4} }\right)^3}=\dfrac{+}{(+)^3}=\dfrac{+}{+}=+>0\hspace{5pt}\Rightarrow\hspace{5pt}$ és un mínim.

El valor cercat era $\boxed{x=+\sqrt{\dfrac{128}{\pi+4}}\ \text{metres}}$ $$x\approx 4,23\ \text{metres}$$.