optimització filferro

Un filferro de 10 metres de longitud es divideix en dos trossos. Amb un es forma un triangle equilàter i amb l’altre un quadrat. Troba la longitud d’aquests trossos perquè la suma de les àrees sigui mínima.

Partim el filferro en dos trossos, un de mida $x$, per al triangle, i l’altre de mida $10-x$, per al quadrat. Tots dos sumen $10$ metres.

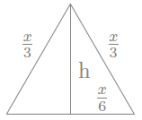
$$\left.\begin{array}{l} \text{El costat del triàngle serà } \dfrac{x}{3} \ \text{La seva altura}h=\sqrt{\left(\frac{x}{3}\right)^2-\left(\frac{x}{6}\right)^2}=\dfrac{\sqrt{3}x}{6} \ \text{ La seva \’area } \dfrac{1}{2}\cdot\text{base}\cdot\text{alçada}=\dfrac{\sqrt{3}x^2}{36}\ u^2 \end{array}\right.$$
El costat del quadrat serà $\dfrac{10-x}{4}$ i per tant la seva àrea $\dfrac{(10-x)^2}{16}\ u^2$

La funció suma de les dues àrees vindrà donada per $f(x)=\dfrac{\sqrt{3}x^2}{36}+\dfrac{(10-x)^2}{16}$

Derivem i igualem a zero per obtenir els possibles màxims i mínims:

$$f'(x)=\dfrac{\sqrt{3}x}{18}+\dfrac{x-10}{8}$$

$$\dfrac{\sqrt{3}x}{18}+\dfrac{x-10}{8}=0\hspace{5pt}\Rightarrow\hspace{5pt}\dfrac{(4\sqrt{3}+9 )x-90}{72}=0\hspace{5pt}\Rightarrow\hspace{5pt}(4\sqrt{3}+9)x-90=0\hspace{5pt}\Rightarrow$$

$$\Rightarrow\hspace{5pt}x=\dfrac{90}{4\sqrt{3}+9}\hspace{5pt}\Rightarrow\hspace{20pt} \boxed{x=\dfrac{810-360\sqrt{ 3}}{33}\ m\approx5,6504\ m}$$

Fem servir la segona derivada per comprovar que realment és un mínim:

$f”(x)=\dfrac{\sqrt{3}}{18}+\dfrac{1}{8}>0$ A continuació, és un mínim.

I l’altre tros és $\boxed{10-x=\dfrac{360\sqrt{3}-480}{33}\ m\approx4,3496\ m}$