Exercici càlcul d’àrea

Sigui $f$ la funció definida per $f(x)=\left\{\begin{array}{ccc} 2x+4 & \text{si} & x<0 \\ (x-2)^2 & \text{ si} & x\geq 0 \end{array}\right.$

a) Calcula els punts de tall de la gràfica de $f$ amb l’eix d’abscisses i esbossa la gràfica de la funció.

• Si $x<0\hspace{5pt}\Rightarrow\hspace{5pt} 2x+4=0 \hspace{5pt}\Rightarrow\hspace{5pt} \boxed{x=-2}$
• Si $x\geq 0\hspace{5pt}\Rightarrow\hspace{5pt} (x-2)^2=0 \hspace{5pt}\Rightarrow\hspace{5pt} x-2=0 \hspace{5pt}\Rightarrow \hspace{5pt} \boxed{x=2}$
  
  $\Rightarrow\hspace{5pt} f(x)$ talla l’eix d’abscises a $(-2,0)$ i a $(2,0)$.

El primer tros de la funció és una equació lineal, una línia recta, que talla a l’eix d’abscises al punt $(-2,0)$, amb pendent $+2$ i ordenada a l’origen $4$, és a dir, talla a l’eix d’ordenades al punt $(0,4)$. Amb això n’hi ha prou per esbossar-la.

El segon tros és la paràbola $y=x^2$ desplaçada dues unitats cap a la dreta, essent el seu vèrtex el punt $(2,0)$ i passant pels punts $(0,4)$ i $(4,4)$.

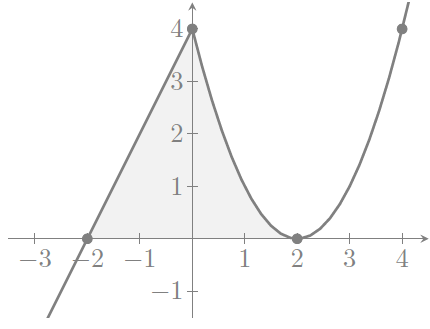
b) Troba l’àrea del recinte limitat per la gràfica de f i per l’eix d’abscisses.

$$\text{Àrea}=\int_{-2}^2 f(x)\ dx=\int_{-2}^02x+4\ dx+\int_0^2(x-2)^2\ dx=$$

$$=\left[x^2+4x\right]_{-2}^0+\left[\dfrac{(x-2)^3}{3}\right]_0^2=$$

$$=0-(4-8)+\left(\dfrac{0}{3}-\dfrac{-8}{3}\right)=4+\dfrac{8}{3}=\dfrac{20} {3}\ u^2$$

Nota: l’àrea del primer tros també es podria haver calculat, per ser un triangle, amb $\dfrac{base\times altura}{2}=\dfrac{2\cdot4}{2}=4\ u^2$.