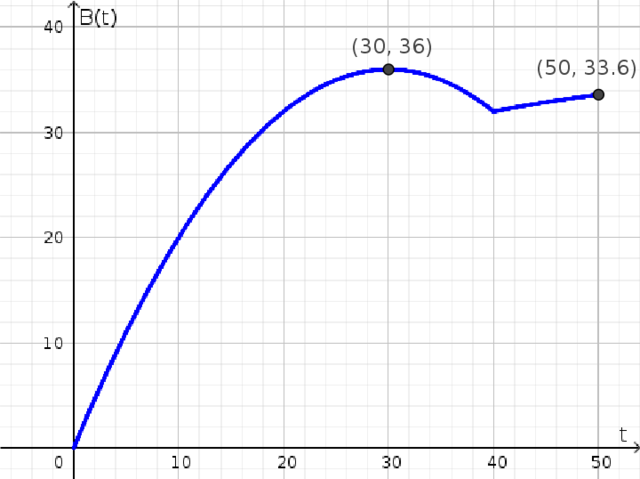
El benefici, en milers d’euros, que ha obtingut una almàssera (Molí que mol les olives reduint-les a pasta per a obtenir-ne l’oli) al llarg de 50 anys de vida ve donat per l’expressió $$B(t)=\left\{\begin{array}{lr}-0.04t^2+2.4t & 0 \leq t < 40 & \\ \displaystyle\frac{40t-320}{t} & 40 \leq t \leq 50\end{array}\right.$$ on $t$ és el temps transcorregut.

Estudiï la continuïtat i la derivabilitat de la funció $B (t)$ en l’interval $[0,50]$.

continuïtat

$-0.04t ^ 2 + 2.4t$ és contínua en $\RR$ i per tant en $(0,40)$

$\frac{40t-320}{t}$ és contínua en $\RR -{0}$ i per tant en $(40,50)$

Vegem la contiuïtat en $t = 40$

• $B (40) = \displaystyle\frac{40 \cdot 40 -320}{40} = 32$
• $\displaystyle\lim_{x \rightarrow 40^-} B (t) = – 0.04 \cdot 40 ^ 2 + 2.4 \cdot 40 = 32$
• $\displaystyle\lim_{x \to 40^+} B (t) = \frac{40 \cdot 40 -320}{40} = 32$

Com els $3$ resultats anteriors coincideixen, la funció és contínua en $t = 40$ i per tant, és contínua en tot l’interval $[0,50]$.

derivabilitat

En $(0,40)$ és derivable i la seva derivada és $-0.08t + 2.4$

En $(40,50)$ és derivable i la seva derivada és $\displaystyle\frac{40 \cdot t – (40t-320) \cdot 1}{t^2} = \frac{320}{t^2}$

Vegem la derivabilitat en $t = 40$

• $B^{\prime}(40^-) = – 0.08 \cdot 40 + 2.4 = -0,8$

• $B^{\prime}(40^+) = \displaystyle\frac{320}{40^2} = 0.2$

Com que no coincideixen les derivades laterals, no és derivable en $t = 40$

Per tant, $B (t)$ és derivable en $(0,50) – {40 }$ i la seva derivada és:

$$B (t) = \left\{\begin{array}{lr}-0.08t + 2.4 & 0 \leq t <40 & \\ \displaystyle\frac{320}{t^2} & 40 <t <50\end {array}\right.$$

Estudiï la monotonia de la funció $B (t)$ i determini en quin moment van ser grans els beneficis de l’almàssera, així com el benefici màxim.

$$-0.08t + 2.4=0 \longrightarrow t=\frac{2.4}{0.08}=30
\frac{320}{t^2} =0 \longrightarrow\ \mathrm{Sense Solució}$$

Els intervals a considerar són:

$$(0,30) (30,40) (40,50)$$
Prenem un punt de cada interval i analitzem el signe de la derivada

• $1 \in (0,30) \longrightarrow -0.08 \cdot 1 + 2.4 >0 \longrightarrow\ \mathrm{CREIX}$

• $35 \in (30,40) \longrightarrow -0.08 \cdot 35 + 2.4 <0 \longrightarrow\ \mathrm{DECREIX}$

• $45 \in (40,50) \longrightarrow \frac{320}{45^2} >0 \longrightarrow\ \mathrm{CREIX}$

Tenim un màxim local en $t=30$ (El vèrtex de la paràbola) i un altre màxim local en $t = 50$ (el punt més alt del segon tros)

• $B(30)=-0.04 \cdot 40^2+2.4 \cdot 30 = 36$

• $B(50)=\displaystyle\frac{40 \cdot 50-320}{50} = 33.6$

Per tant, els màxims beneficis són 36000 euros, que s’obtenen als 30 anys.