Problema 6

Sea $P(t)$ el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo $t$, medido en meses:

$$P(t) = \left\{\begin{array}{lcc}
t^2 & si & 0 \leq t \leq 5 \\
\frac{100t-250}{t+5} & si & t >5
\end{array}\right.$$

a) Estudie la continuidad de la función $P$.

En $(0,5)$  es continua por ser polinómica

 En $(5,+\infty)$  se trata de una función racional que sólo es discontinua en $t = -5$  (punto que anula el denominador), por tanto en $(5,+\infty)$  es continua.

$P(5) =5^2 = 25$

$\displaystyle\lim_{t\to 5^-} P(t) = \lim_{t\to5} t^2 = 5^2=25$

$\displaystyle\lim_{t \to5^+} P(t) = \lim_{t\to5} \frac{100t-250}{t+5} = \frac{250}{10}=25$

Coinciden ambos límites, por tanto es continua en $t = 5$

b) Estudie la derivabilidad de P en $t = 5$.

Derivabilidad en $t = 5$

La función derivada sería:

$P(t)=\left\{\begin{array}{lcc}
2t & si & 0 < t < 5 \\ \frac{750}{(t+5)^2} & si & t >5
\end{array}\right.$

Calculamos derivadas laterales en  $t = 5$

$P'(5^{5^-}) =2\cdot5 = 10$

$P'(5^{5^+}) = \frac{750}{(5+5)^2} = 7.5$

lo coinciden las derivadas laterales, por tanto no es derivable en $t = 5$

c) Estudie la monotonía de dicha función e interprete la evolución del porcentaje de células afectadas.

Dado que se trata de funciones conocidas (parábola e hipérbola), podríamos dibujarla y a vista de la gráfica determinar la monotonía. No obstante, vamos a estudiar la monotonía mediante derivadas, como si se tratase de funciones desconocidas:

En el primer trozo $P(t)=0 \Longrightarrow 2t=0 \Longrightarrow t=0$

El intervalo a estudiar es $(0,5)$. Si tomamos un punto, por ejemplo $t = 2$, vemos que $P(2) = 4 >0$ , por tanto creciente en $(0, 5)$

En el segundo trozo, si hacemos $P(t)=0 \Longrightarrow \frac{750}{(t+5)^2}=0 \Longrightarrow 750=0$, es decir, ninguna solución (lo cual quiere decir que será siempre creciente o siempre decreciente).
Si tomamos un punto, por ejemplo $t = 6$, vemos que $P(6) = \frac{750}{11^2} >0$ , por tanto creciente en $(5,+\infty)$. Concluimos que la función siempre es creciente.

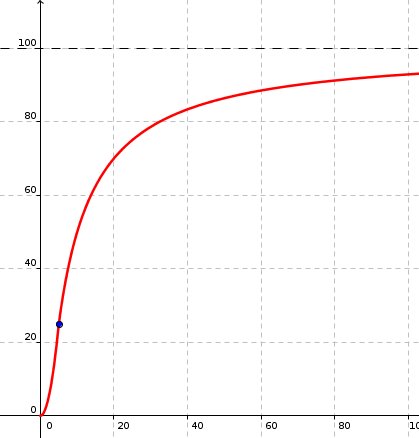
El porcentaje de células sigue creciendo siempre, sin llegar nunca al $100\%$  pues hay una asíntota en $y=100$.

d)  ¿En algún momento el porcentaje de células afectadas podría valer 50?

Veamos cuándo el porcentaje es de 50

Debemos mirarlo en el segundo trozo, pues el primero llega como máximo a $5^2 = 25$

$\displaystyle\frac{100t-250}{t+5}=50 \Rightarrow 100t-250=50(t+5) \Rightarrow t=10$

A los 10 meses el porcentaje de células será del $50\%$.